حجم، مساحت و محیط شکل های هندسی مختلف

 

جهت مشاهده تصویر با ابعاد واقعی و با کیفیت بر روی آن کلیک کنید.
 

 

ریاضی چیست؟

 

ریاضیات عموما مطالعه الگوی ساختار، تحول، و فضا تعریف شده است؛ بصورت غیر رسمی تر، ممکن است بگویند مطالعهاعداد و اشکال است.تعریف ریاضیات بر حسب وسعت دامنة آن و نیز بسط دامنة فکر ریاضی تغییر کرده است. 

ریاضیات زبانی خاص خود دارد،که در آن به جای کلمات و علائم نقطه گذاری از اعداد و نمادها استفاده میشود. در منظر صاحبان فکر، تحقیق بدیهیات ساختارهای مجرد تعریف شده، با استفاده از منطق و نماد سازی ریاضی میباشد. 
نخستین اعداد ثبت شده خطوطی بودند که روی یک چوب کشیده میشدند،که اصطلاحا آنها را چوبخط مینامیدند.این خطوط به شکل دسته های کوچک دو یا پنج تایی کشیده میشدند.سرانجام به این دسته ها نمادهای خاصی اختصاص داده شد(5،2 و غیره)و یک دستگاه حساب ایجاد شد. 
ریاضیدانان نمادهای خاصی را به جای کلماتی از قبیل به اضافه و مساوی است با وضع کردند،همچنین کلمات خاصی را برای بیان مفاهیم جدید ابداع کردند. 
چنانکه زمانی آن ار علم عدد ، زمانی علم فضا ، گاه علم کمیات ، و زمانی علم مقادیر متصل و منفصل خوانده اند.ریاضیات درباره حساب، هندسه ، جبر و مقابله بحث می کند که ما در اینجا به سراغ تاریخ هر یک از آنها می رویم. 
ساختارهای بخصوصی که در ریاضیات مورد تحقیق و بررسی قرار میگیرند اغلب در علوم طبیعی منشاء دارند، و بسیار عمومی در فیزیک، ولی ریاضیات ساختارهای دلایلی را نیز بررسی می نماید که بصورت خالص در مورد باطن ریاضی است، زیرا ریاضیات می توانند برای مثال، یک عمومیت متحد شده را برای زیر-میدانهای متعدد، یا ابزارهای مفید را برای محاسبات عمومی، فراهم نماید. در نهایت، ریاضیدانان بسیاری در مورد مطالبی که مطالعه می نمایند که منحصرا دلایل علمی محض داشته، ریاضیات را بصورت هنری برای پروراندن علم، صرف نظر از تجربی یا کاربردی، می نگرند. 
حساب ، علم اعداد است. واژه انگلیسی حساب ، از کلمه ای یونانی به معنای اعداد گرفته شده است. 
در آغاز شهرنشینی ، انسان گوسفندان ، گاوها و سایر حیوانات خود را با انگشتانش می شمرد. در واقع کلمة دیژیت که برای شمارش اعداد از 0 تا 9 به کار می رود، از یک کلمة لاتین به معنای انگشت گرفته شده است. 
بعدها انسان با علامت زدن روی چوب یا درخت ، اشیاء را می شمرد. اما این روش به زودی جای خود را به استفاده از علامتهایی باری هر یک از اعداد داد. 
هندسه مطالعه انواع مختلف اشکال و خصوصیات آنهاست. همچنین مطالعه ارتباط میان اشکال ، زوایا و فواصـل است.

مسائل حل نشده ریاضی با ظاهری ساده

ریاضیات مملو از مسائلی است که هنوز بعد از گذشت سال­‌ها بی‌­پاسخ مانده­‌اند؛ اما بعضی از این مسائل ظاهر بسیار ساده‌­ای دارند و برای همه‌­ی افراد قابل درک هستند.

 

در ریاضیات به مسائلی که تاکنون اثبات یا رد نشده‌اند، «مسئله‌های باز» گفته می‌شود. اغلب این مسائل در سطوح بالای ریاضی مطرح می‌شوند و دارای ظاهری مشکل هستند؛ مانند مسائل هزاره که حل هرکدام از آن‌ها یک میلیون دلار به جیب شما سرازیر می‌کند؛ اما شاید اهمیت حل آن‌ها بیشتر از جایزه‌‌ باشد؛ همان‌طور که گریگوری پرلمان وقتی در سال ۲۰۰۶ یکی از مسائل هزاره را حل کرد، یک میلیون دلار را نپذیرفت. او گفت «من همه‌ی آنچه را که می‌خواهم، در اختیار دارم. من می‌توانم هستی را کنترل کنم؛ پس به من بگویید چرا باید دنبال یک میلیون دلار باشم؟».

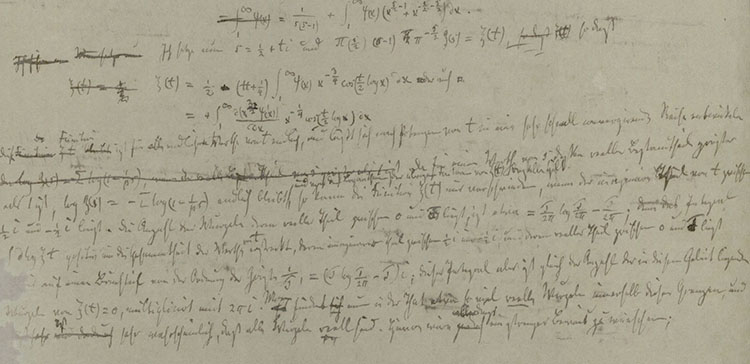
یکی دیگر از همین مسائل که به فرضیه‌ی ریمان معروف است؛ از مشهورترین و مهم‌ترین مسائل حل نشده‌ی ریاضی به شمار می‌رود که نتایجی را در ارتباط با توزیع اعداد اول در بر دارد. عکس بالا، دست‌خط ریمان را در سال ۱۸۵۹ نشان می‌دهد؛ زمانی که فرضیه‌ی مهم خود را بیان کرد. اما فارغ از تمام موارد یادشده، مسائلی وجود دارند که با وجود ظاهر ساده و قابل فهم، حل‌نشده باقی مانده‌اند؛ مسائلی که هر‌کس با دانش دبیرستانی می‌تواند آن‌ها را درک و روی کاغذ امتحان کند. در این مقاله به هفت نمونه از مسائل این‌چنینی خواهیم پرداخت.

لطفاً برای مشاهده این 7 مسئله حل نشده به ادامه مطلب مراجعه کنید.

منبع:                                                   www.zoomit.ir

آموزش ساده حل کسر های مصری

در این مقاله بهترین راه های حل کسر مصری آورده شده

است.برای دانلود کلیک کنید.

هندسه عنکبوتی

 

تار عنکبوت شبکه‌ای از رشته‌های پروتئینی است که توسط عنکبوتها تنیده می‌شود. این پروتئین سرشار از آمینو اسیدهای آلانین و گلیسین است. بیشتر رشته‌های پلی پپتیدی سازندهٔ این پروتئین، به صورت صفحات بتا آرایش یافته‌اند. این صفحات در زمینه‌ای از رشته‌های آمینو اسید به صورت صفحات آلفا جای گرفته‌اند. مارپیچ‌های آلفا با بی‌نظمی زیادی به هم پیچیده‌اند و همین بی‌نظمی باعث خاصیت کش سانی تار می‌شود. یکی از ویژگی‌های جالب تار عنکبوت این است که مقدار زیادی نمک و مواد ضد باکتری و ضد قارچ دارد که در برابر حملهٔ باکتری‌ها و قارچ‌ها از آن محافظت می‌کند.

تقویم ذهنی سال 97

 

هندسه زنبوری

🔸زنبور عسل نه تنها برای ساخت خانه ی خود از شش ضلعی استفاده می‌کند، بلکه برای ساخت کندوی خود نیز از الگوی منظمی استفاده می‌کند.

سلام

سلام بر شما دوستان گرامی.

لطفاً از تمام مطالب سایت بازدید کنید.

و همچنین از دیگر صفحات سایت دیدن فرمایید.(در پایین صفحه)